Probability Theory Poker
- Probability Theory Pierre De Fermat
- Probability Theory Poker Game
- Probability Theory Poker Strategy
- Probability Theory Power System Reliability
- Probability Theory Poker Rules
- Probability Theory Probability
EmileBorel: The Forgotten Father of Game Theory?
In 1921, Emile Borel, a French mathematician, published several papers onthe theory of games. He used poker as an example and addressed the problemof bluffing and second-guessing the opponent in a game of imperfectinformation. Borel envisioned game theory as being used in economic andmilitary applications.Borel's ultimate goal was to determine whether a 'best' strategy for agiven game exists and to find that strategy. While Borel could be arguablycalled as the first mathematician to envision an organized system forplaying games, he did not develop his ideas very far. For that reason,most historians give the credit for developing and popularizing gametheory to John Von Neumann, who published his first paper on game theoryin 1928, seven years after Borel.
John Von Neumann
Born in Budapest, Hungary, in 1903, Von Neumann distinguished himself fromhis peers in childhood for having a photographic memory, being able tomemorize and recite back a page out of a phone book in a few minutes.Science, history, and psychology were among his many interests; hesucceeded in every academic subject in school.
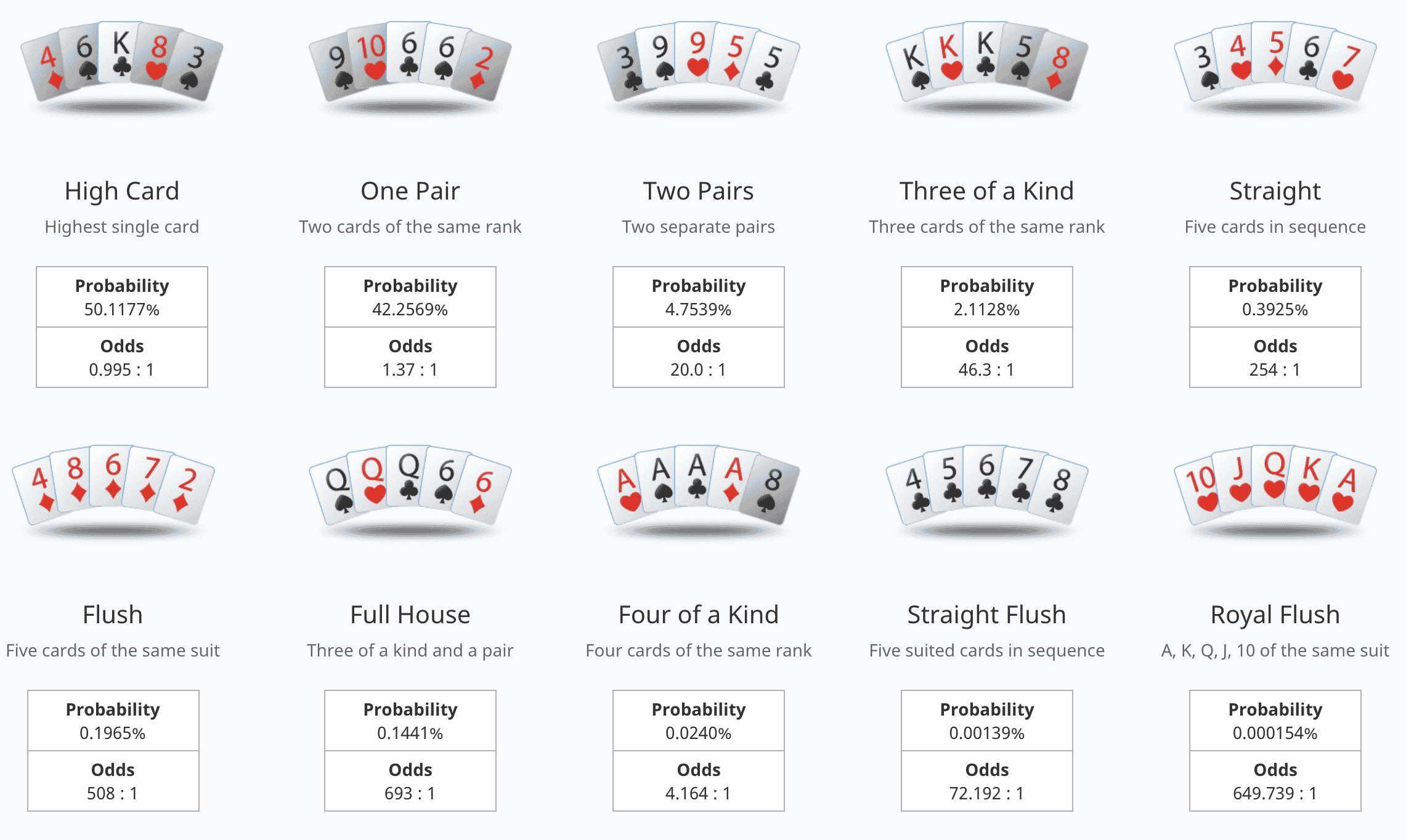
Probability Theory Probability and the ability to understand and predict human behavior are the two important keys to playing and winning at Texas Holdem. Learning how to read your opponents comes with practice, a keen sense of observation, and years of experience. Review of Probability Theory Arian Maleki and Tom Do Stanford University Probability theory is the study of uncertainty. Through this class, we will be relying on concepts from probability theory for deriving machine learning algorithms. These notes attempt to cover the basics of probability theory at a level appropriate for CS 229. The mathematics of gambling are a collection of probability applications encountered in games of chance and can be included in game theory.From a mathematical point of view, the games of chance are experiments generating various types of aleatory events, the probability of which can be calculated by using the properties of probability on a finite space of events. Poker probability. The game of poker is quite popular with players today. Mathematics and the probability theory can be applied even to poker. In poker the probability of every type of five card hand can be calculated. This theory is particularly known as the poker probability. Frequency of the five card hands. Although the mathematical theory of probability has its roots in attempts to analyze games of chance by Gerolamo Cardano in the sixteenth century, and although others built on probability theory after Pascal and Fermat, the story of probability theory properly begins with Pascal, Fermat, and a dispute between gamblers in 1654.

He published his first mathematical paper in collaboration with his tutorat the age of eighteen, and resolved to study mathematics in college. Heenrolled in the University of Budapest in 1921, and over the next fewyears attended the University of Berlin and the Swiss Federal Instituteof Technology in Zurich as well. By 1926, he received his Ph.D. inmathematics with minors in physics and chemistry.
By his mid-twenties, von Neumann was known as a young mathematical genius and his fame had spread worldwide in the academic community. In 1929, hewas offered a job at Princeton. Upon marrying his fiancee, Mariette,Neumann moved to the U.S. (Agnostic most of his life, Von Neumann acceptedhis wife's Catholic faith for the marriage, though not taking it veryseriously.)
In 1935, Mariette gave birth to Von Neumann's daughter, Marina. Two yearslater, Mariette left Von Neumann for J. B. Kuper, a physicist. Within ayear of his divorce, Von Neumann began an affair with Klara Dan,his childhood sweetheart, who was willing to leave her husband for him.
Von Neumann is commonly described as a practical joker and always the lifeof the party. John and Klara held a party every week or so, creating akind of salon at their house. Von Neumann used his phenomenal memory tocompile an immense library of jokes which he used to liven up aconversation. Von Neumann loved games and toys, which probably contributedin great part to his work in Game Theory.
An occasional heavy drinker, Von Neumann was an aggressive and recklessdriver, supposedly totaling a car every year or so. According to WilliamPoundstone's Prisoner's Dilemma, 'an intersection in Princeton wasnicknamed 'Von Neumann Corner' for all the auto accidents he had there.'(p.25)
His colleagues found it 'disconcerting' that upon entering an office wherea pretty secretary worked, von Neumann habitually would 'bend way wayover, more or less trying to look up her dress.' (Steve J. Heims, JohnVon Neumann and Norbert Wiener: From Mathematics to the Technologies ofLife and Death, 1980, quoted in Prisoner's Dilemma, p.26) Somesecretaries were so bothered by Von Neumann that they put cardboard partitions at thefront of their desks to block his view.
Despite his personality quirks, no one could dispute that Von Neumann wasbrilliant. Beginning in 1927, Von Neumann applied new mathematical methodsto quantum theory. His work was instrumental in subsequent 'philosophical'interpretations of the theory.
Probability Theory Pierre De Fermat
For Von Neumann, the inspiration for game theory was poker, a game heplayed occasionally and not terribly well. Von Neumann realized that pokerwas not guided by probability theory alone, as an unfortunate player whowould use only probability theory would find out. Von Neumann wanted toformalize the idea of 'bluffing,' a strategy that is meant to deceive theother players and hide information from them.
In his 1928 article, 'Theory of Parlor Games,' Von Neumann firstapproached the discussion of game theory, and proved the famous Minimaxtheorem. From the outset, Von Neumann knew that game theory would proveinvaluable to economists. He teamed up with Oskar Morgenstern, an Austrianeconomist at Princeton, to develop his theory.
Their book, Theory of Games and Economic Behavior, revolutionizedthe field of economics. Although the work itself was intended solely foreconomists, its applications to psychology, sociology, politics, warfare,recreational games, and many other fields soon became apparent.
Although Von Neumann appreciated Game Theory's applications toeconomics, he was most interested in applying his methods to politics andwarfare, perhaps stemming from his favorite childhood game, Kriegspiel, achess-like military simulation. He used his methods to model the Cold Warinteraction between the U.S. and the USSR, viewing them as two players ina zero-sum game.
Probability Theory Poker Game
From the very beginning of World War II, Von Neumann was confident of theAllies' victory. He sketched out a mathematical model of the conflictfrom which he deduced that the Allies would win, applying some of themethods of game theory to his predictions.
In 1943, Von Neumann was invited to work on the Manhattan Project. VonNeumann did crucial calculations on the implosion design of the atomicbomb, allowing for a more efficient, and more deadly, weapon. VonNeumann's mathematical models were also used to plan out the path thebombers carrying the bombs would take to minimize their chances of beingshot down. The mathematician helped select the location in Japan to bomb.Among the potential targets he examined was Kyoto, Yokohama, and Kokura.
'Of all of Von Neumann's postwar work, his development of the digitalcomputer looms the largest today.' (Poundstone 76) After examining theArmy's ENIAC during the war, Von Neumann came up with ideas for a bettercomputer, using his mathematical abilities to improve the computer's logicdesign. Once the war had ended, the U.S. Navy and other sources providedfunds for Von Neumann's machine, which he claimed would be able toaccurately predict weather patterns.
Capable of 2,000 operations a second, the computer did notpredict weather very well, but became quite useful doing a set ofcalculations necessary for the design of the hydrogen bomb. Von Neumann is also credited with coming up with the idea of basing computercalculations on binary numbers, having programs stored in computer'smemory in coded form as opposed to punchcards, and several othercrucial developments. Von Neumann's wife, Klara, became one of the firstcomputer programmers.
Von Neumann later helped design the SAGE computer system designed todetect a Soviet nuclear attack
In 1948, Von Neumann became a consultant for the RAND Corporation. RAND(Research ANd Development) was founded by defense contractors and theAir Force as a 'think tank' to 'think about the unthinkable.' Their mainfocus was exploring the possibilities of nuclear war and the possiblestrategies for such a possibility.
Von Neumann was, at the time, a strong supporter of 'preventive war.'Confident even during World War II that the Russian spy network hadobtained many of the details ofthe atom bomb design, Von Neumann knew that it was only a matter of timebefore the Soviet Union became a nuclear power. He predicted that wereRussia allowed to build a nuclear arsenal, a war against the U.S. would beinevitable. He therefore recommended that the U.S. launch a nuclear strikeat Moscow, destroying its enemy and becoming a dominant world power, so asto avoid a more destructive nuclear war later on. 'With the Russians it isnot a question of whether but of when,' he would say. An oft-quoted remarkof his is, 'If you say why not bomb them tomorrow, I say why not today? Ifyou say today at 5 o'clock, I say why not one o'clock?'
Just a few years after 'preventive war' was first advocated, it became animpossibility. By 1953, the Soviets had 300-400 warheads, meaning that anynuclear strike would be effectively retaliated.
In 1954, Von Neumann was appointed to the Atomic Energy Commission. A yearlater, he was diagnosed with bone cancer. William Poundstone'sPrisoner's Dilemma suggests that the disease resulted from the radiation VonNeumann received as a witness to the atomic tests on Bikini atoll. 'A number ofphysicists associated with the bomb succumbed to cancer at relativelyearly ages.' (p. 189)
Von Neumann maintained a busy schedule throughout his sickness, even whenhe became confined to a wheelchair. It has been claimed by some that thewheelchair-bound mathematician was the inspiration for the character ofDr. Strangelove in the 1963 film Dr. Strangelove or: How I Learned to StopWorrying and Love the Bomb.
Probability Theory Poker Strategy
Von Neumann's last public appearance was in February 1956, when PresidentEisenhower presented him with the Medal of Freedom at the White House. InApril, Von Neumann checked into Walter Reed Hospital. He set up office inhis room, and constantly received visitors from the Air Force and theSecretary of Defense office, still performing his duties as a consultantto many top political figures.
John von Neumann died February 8, 1957.
His wife, Klara von Neumann, committed suicide six years later.
Dr. Marina von Neumann Whitman, John's daughter from his first marriage,was invited by President Nixon to become the first woman to serve on thecouncil of economic advisers.
Probability Theory
Probability and the ability to understand and predict human behavior are the two important keys to playing and winning at Texas Holdem. Learning how to read your opponents comes with practice, a keen sense of observation, and years of experience. The knowledge of Texas Holdem probability theory can and should be learned before you sit down with a pile of chips in front of you. For example the odds of catching your flush or straight, the odds of getting an overcard, or the proportion (or percentage) of times you're going to match a card on the flop to your pair of cards in your hand, and the percentage of times you can expect to lose if you do not catch your set on the flop holding a small pair are a few extremely important factors in learning how to play Texas Holdem Poker. Knowledge of these statistics is probably the most important key to winning and is often the difference between winning and losing. In online games especially without any face to face confrontations, statistical knowledge becomes the main factor when choosing whether to bet, call, or fold.
Here are some terms that you'll hear on this site and whenever you're talking about poker odds...
Outs
The number of cards left in the deck that will improve your hand. 'I had four diamonds on the turn, so I had only 9 outs left to finish that flush.'
Pot Odds
The odds you get when analyzing the current size of the pot vs. your next call. 'There's $240 already in the pot, and another $12 bet coming at me, so my pot odds are good if I hit that diamond flush'
Bet Odds
The odds you get as a result of evaluating the number of callers to a raise. 'With a 1 in 5 chance of hitting it, and knowing all six of these guys are planning on calling my bet, my bet odds are good too.'
Implied Odds
The odds you are getting after the assumed result of betting for the remainder of the hand. 'Since I think these guys are going to call on the turn and river, my implied odds are excellent.'
In Texas Hold 'Em, you commonly use outs and pot odds the most. This is also the starting point for those who want to learn about poker odds. To those out there who 'are not exactly great mathematicians', you better get good because that is how it's done. At this point it's only simple division The numerator will be the number of outs you have. The denominator is the number of cards left that we haven't seen. The result will be the percentage chance of making one of those outs. Therefore, the most math you'll be doing will be dividing small numbers by 50 (pre-flop), 47 (after the flop), or 46 (after the turn).
Before we move on, we would like to take the opportunity to clarify one point of statistical interest. A lot of you might wonder why we never factor the opponents' cards or the nonused cards (referred to as the burn cards) when figuring out the denominator in our mathematical interpretation. The answer is very simple. We only consider 'unseen cards' in all our mathematical calculations. If you saw what the burn cards (or unused cards) were, or an opponent showed you his hand, you would know that those cards are not going to be drawn and could use that information in your calculations. We typically do not know what they have, so we don't even think about it when talking about odds.
Pot odds are as easy as computing outs. You compare your outs or your chance of winning to the size of the pot. If your chance of winning is significantly better than the ratio of the pot size to a bet, then you have good pot odds. If it's lower, then you have bad pot odds. For example, say you are in a $5/$10 holdem game with Jack-Ten facing one opponent on the turn. You have an outside straight draw with a board of 2-5-9-Q, and only the river card left to make it. Any 8 or any King will finish this straight for you, so you have 8 outs (four 8's and 4 K's left in the deck) and 46 unseen cards left. 8/46 is almost the same as a 1 in 6 chance of making it. Your sole opponent bets $10. Now you have to decide if calling that bet is a good idea or is folding the move to make here. How do we know what to do? Simple – look for the math to help you make the right decision. Now if you take a $10 bet you could win $200. $200/$10 is 20, so you stand to make 20x more if you call. 1/6 is a greater number than 1/20 so the math is telling you to call this bet into you. What about raising into this same scenario? Well then you would be putting in $20 to make back $220 or 1/11 so again the real gambler would raise since he could either win with his straight or win when his opponent folds. However if his opponent re-raised another $60 then you would be getting only 1 in 4.67 to one odds and that is not enough money to call – so now it would be time to fold.
Another clarification is in order right about now ... you see there are a lot of players want to somehow factor in money they wagered on previous rounds in all their calculations. With the last example, you probably had already invested a significant portion of that $200 pot. Let's say $50. Does that mean you should play or fold because of that money you already have in there? $50/$200? Not at all. That's not your money anymore! It's in a pool of money to be given to the winner. You have no 'stake' to any of the funds you have already put in the pot. This is exactly where amateur Texas Holdem players make their biggest tactical mistake. They think about all the money they have put in that pot and chase after the pot even though their mathematical chances of winning are slim to none. The only stake you might have is totally mental and has no bearing on hard statistics.
The next step is to use bet odds and implied odds. That's tougher, because it involves predicting reactions of other players. With bet odds, you try to factor in how many people are going to call a raise. With implied odds, you're thinking about reactions for the rest of the game. One last example on implied odds...
Say it's another $5/$10 holdem game and you have a four flush on the flop. Your neighbor bets, and everyone else folds. The pot is $50 at this point. First you figure your chance of hitting your flush on the turn, and it comes out to about 19.1% (about 1 in 5). You have to call this $5 bet vs a $50 pot, so that's a 10x payout. 1/5 is higher than 1/10, so bet odds are okay, but you must consider that this guy's going to bet into you on the turn and river also. That's the $5 plus two more $10 bets. So now your facing $25 more till the end of the hand. So you have to consider your chances of hitting that flush on the turn or river, which makes it about 35% (better than 1 in 3 now), but you have to invest $25 for a finishing pot of $100. $100/$25 is 1 in 4. That's pretty close. But there's more!... if you don't make it on the turn, it'll change your outs and odds! You'll have a 19.6% chance of hitting the flush (little worse than 1 in 5), but a $20 investment for a finishing pot of $100! $100/$20 is 1 in 5. So the chances would take a nasty turn if you didn't hit it! What's makes it more complicated is that if you did hit it on the turn, you could raise him back, and get an extra $20 or maybe even $40 in the pot.
As you can see I could imagine additional scenarios that would make it impossible for you to call. What you have to do is to master simple outs and pot odds, and remember that bet and implied odds are just extended versions of those odds. If you sit and think about these things while you play, it'll come to you eventually without any help at all.
Example number one: playing with a pocket pair.
You start with a pair of Aces in the pocket. You are holding the top pair. The flop however, doesn't contain another Ace.
Lesson 1: What are my chances of getting an Ace on the turn?
You need to just figure out the number of outs and divide it by the number of cards in the deck. There's 2 more Aces. There's 47 more cards since you've seen five already (two in your hand and three on the flop). The answer is 2/47, or 0.0426, let’s say close to 4.3%.

Lesson 2:No luck on the turn, how 'bout the river?
Still 2 Aces left, but one less card in the deck bringing the grand total to 46. What's 2/46? That's .0434, which is also a little more than 4.3% Your chances didn't change much.
Lesson 3:Now what if I wanted to get 4 Aces! What are my chances of that happening?
Since we're trying to figure out the chances of getting one on the turn AND another one on the river, and not getting one on EITHER the turn or river, we don't have to reverse our thinking. Just multiply the probability of each event happening. Chances of getting that first Ace on the turn was 0.0426 and the chance of getting a second Ace on the river would be 1/46, because there would only be one Ace left in the deck. That's about 0.0217, or 2.2%. To get the answer, multiply these to together .0426 X .0217 is about .0009! That's around one-tenth of a percent or one in one thousand hands that you get pocket Aces to start your hand - not often.
Lesson 4: Hey, what were my chances of getting a pair of Aces to start off with anyway?
Lesson 5: What were my chances of getting an Ace on the flop?
Now you do have to 'think in reverse' as in the previous example. Figure out the chances of NOT getting a Ace on each successive card flip. First card you have a 48/50 chance (48 non-Ace cards left, 50 cards left in the deck), second card is 47/49, third card is 46/48. Those come out to .96, .959, and .958. Multiply them and get .882, or an 88.2% chance of NOT getting any Aces on the flop. Invert it to figure out what your chances really are and you get .118 or 11.8%. This will be your chance to get one more Ace on the flop.
Example number two: 'The straight draw'
You start with a Jack of Spades and a Ten of Spades. You get a rainbow flop with a Queen of Spades, a Three of Diamonds, and a Nine of Clubs. You've got a straight draw.
Lesson 1: What are my chances of hitting it on the next card?
Same as before, but with different outs. A King or an Eight will complete your hand. There are presumably four of each left in the deck. You've got 8 outs. The chance of getting one of them on the turn is 8 over 47, because there's 47 cards left in the deck. That comes out to about .170, or around 17%.
Lesson 2: I didn't get it on the turn! What are my chances now!?
There's still 8 cards left in the deck that'll help you, but 46 cards left in the deck. That's 8 over 46. It changes to .174. It's improved to a whopping 17.4%!
Lesson 3: I should of thought about my total chances first, I'm such an idiot. What are my chances of getting that card on the turn OR the river?
Once again we'll have to calculate the chances of a King or Eight NOT appearing, so we can do it like the last problem (in this case, {39/47} X {38/46}). Or, since we've already figured out our chances in the previous two lessons, we can just invert the probabilities and multiply 'em. You had a .170 chance on the turn, and a .174 on the river. By inverting, I mean subtracting them from one. Now we've got .830 and .826! Multiply and get .686! That's our chance of NOT hitting our card at all. So invert it again and get .314, or 31.4%. So drawing to an open ended straight draw is 31.4% - now that I like.
Example number three: 'Top two pair'
You get dealt a King of Diamonds and a Nine of Hearts. The flop is lookin' pretty good for you with a King of Spades, a Nine of Clubs, and a Four of Clubs. Top two pair!
Lesson 1: What are my chances of getting a full house on the turn?
To get a full house, you need another King or Nine to pop up. There are presumably two of each left in the deck. So you've got 4 outs. After the flop there's always 47 cards unaccounted for. 4/47 is around .085 or an 8.5% chance of you getting that boat.
Lesson 2: What are my chances of getting a full house on the river?
If it didn't happen on the turn, your chances usually don't change all too much, but let's check. You've still got 4 outs and now 46 unseen cards left. 4/46 is about .087 or around an 8.7% chance of hitting it on the river. A .2% difference. Sorry.
Lesson 3: How about the chances of getting the boat on the turn OR the river?
Probability Theory Power System Reliability
Like the previous examples, to figure your chance of something happening on multiple events, you need to calculate the chance of it NOT happening first. On the turn it won't happen 43/47 times. On the river it won't happen 42/46 times. 43/47 is .915, and 42/46 is .913. Multiply them and get .835, or 83.5% chance of it not happening. Invert that and you get a 16.5% of getting at least a full house by the showdown.
Probability Theory Poker Rules
Lesson 4: What do you mean by 'at least'?
Since we figured the chances to NOT get dealt a full house, the chances are built in if the turn and river are two Kings, two Nines, or a King and a Nine. If you are dealt two cards both of either King or Nine, it'll be four-of-a-kind and not a King and Nine 33% of the time. Think of it as being dealt one card then the other. What are the chances of the first card matching the second? Whether it's a King or Nine, there will be only one unaccounted for, but two of the other. That's 1/3, or 33%.
Probability Theory Probability
Lesson 5: Then what are my chances of getting four-of-a-kind?
This is a little more abstract. I hope I warmed you up for this with the previous lesson. It doesn't matter which card we're banking on. We need to first get a full house on the turn. According to lesson #1, the chance of that happening is .085. The chance of getting the same card we got on the turn is 1/46. There's only one out, and the usual 46 unseen cards. 1/46 is around .022, or 2.2%. Multiply the two probabilities (.022 X .085) and get .002 or one-fifth of a percent. It will be Kings half of the time and Nines the other half.
That is a lot of information to digest in one shot, but if you are serious about playing poker to win then you have to become a master of odds, and you need to review all the odds over and over again until you know the odds perfectly and you know the odds in any given situation as well. Like anything else, practice makes perfect.